Modellépítés / modellszelekció
- optimális eset: elméletvezérelt modellépítés
- gyakoribb eset: adatvezérelt modellépítés
- döntési pontok: fix hatások és random hatások, random hatáson belül random konstans és random slope -> kevés változó esetén is nagyon komplex lehet!
Javaslatok
- inkább haladjunk a bővebb modell felől
- először random hatások, utána fix hatások tesztelése
- a random hatásoknál érdemes a maximális struktúrát megtartani (feltéve, hogy konvergál)
- a random hatásokat REML, a fix hatásokat ML becsléssel teszteljük (a végső modell paramétereit REML becsléssel számoljuk)
- a modellszelekció történhet likelihoodarány-teszttel vagy pl. AIC-értékek összevetésével
- ha két fix hatás interakciója szerepel a modellben, akkor mindig vegyük be a főhatásokat is, illetve szerepeltessük az interakciót a random struktúrában is
Példa
Egy lehetséges induló modell
- modellezzük a válaszidőt (RT) a próba sorszáma (scTrial) és a személy anyanyelve, illetve a szó szemantikai kategóriája alapján
( model_full <- lmer(scRT ~ scTrial + NativeLanguage*Class +
(1 + scTrial | Subject) +
(1 | Page) + (1 | Word),
data = lexdec_corr) )
## Linear mixed model fit by REML ['lmerMod']
## Formula:
## scRT ~ scTrial + NativeLanguage * Class + (1 + scTrial | Subject) +
## (1 | Page) + (1 | Word)
## Data: lexdec_corr
## REML criterion at convergence: 3573.958
## Random effects:
## Groups Name Std.Dev. Corr
## Word (Intercept) 0.3278
## Subject (Intercept) 0.5310
## scTrial 0.1266 -0.41
## Page (Intercept) 0.2846
## Residual 0.6831
## Number of obs: 1594, groups: Word, 79; Subject, 21; Page, 10
## Fixed Effects:
## (Intercept) scTrial
## -0.28836 -0.03841
## NativeLanguageOther Classplant
## 0.74844 0.04091
## NativeLanguageOther:Classplant
## -0.17005
örök FAQ: miért nem számol az lmer p-értékeket?: ezért
az lmer outputja a regressziós modellek outputjának formátumát követi; mit tegyünk, ha mi ANOVA-stílusú táblázatot szeretnénk?
library(car)
Anova(model_full)
## Analysis of Deviance Table (Type II Wald chisquare tests)
##
## Response: scRT
## Chisq Df Pr(>Chisq)
## scTrial 1.3803 1 0.240055
## NativeLanguage 9.0170 1 0.002675 **
## Class 0.1232 1 0.725551
## NativeLanguage:Class 5.9001 1 0.015140 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Anova(model_full, test.statistic = "F")
## Note: method with signature 'sparseMatrix#ANY' chosen for function 'kronecker',
## target signature 'dgCMatrix#ngCMatrix'.
## "ANY#sparseMatrix" would also be valid
## Analysis of Deviance Table (Type II Wald F tests with Kenward-Roger df)
##
## Response: scRT
## F Df Df.res Pr(>F)
## scTrial 1.3798 1 19.86 0.25403
## NativeLanguage 8.1579 1 19.02 0.01010 *
## Class 0.1214 1 71.94 0.72853
## NativeLanguage:Class 5.8946 1 1482.69 0.01531 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# az SPSS és SAS a Type III felbontást részesítik előnyben
Anova(model_full, type = 3)
## Analysis of Deviance Table (Type III Wald chisquare tests)
##
## Response: scRT
## Chisq Df Pr(>Chisq)
## (Intercept) 2.4452 1 0.1178872
## scTrial 1.3803 1 0.2400554
## NativeLanguage 11.0466 1 0.0008885 ***
## Class 0.1936 1 0.6599082
## NativeLanguage:Class 5.9001 1 0.0151402 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Random hatások tesztelése
- elsősorban akkor szükséges, ha túl komplex az induló modell, és/vagy szélsőséges értékek szerepelnek a varianca-kovariancia mátrixban (pl. 1 vagy -1 közeli korreláció és/vagy 0 szórás)
- az
anova.merModfüggvény használható, de valószínűleg túl konzervatív (szélsőséges esetben akár 2-szerese a p-érték a valósnak) - használhatjuk az AIC (vagy BIC) kritériumot is
# modellek illesztése
( model_r1 <- lmer(scRT ~ scTrial + NativeLanguage*Class +
(1 | Subject) + (0 + scTrial | Subject) +
(1 | Page ) + (1 | Word),
data = lexdec_corr) )
## Linear mixed model fit by REML ['lmerMod']
## Formula: scRT ~ scTrial + NativeLanguage * Class + (1 | Subject) + (0 +
## scTrial | Subject) + (1 | Page) + (1 | Word)
## Data: lexdec_corr
## REML criterion at convergence: 3576.323
## Random effects:
## Groups Name Std.Dev.
## Word (Intercept) 0.3274
## Subject scTrial 0.1263
## Subject.1 (Intercept) 0.5322
## Page (Intercept) 0.2849
## Residual 0.6831
## Number of obs: 1594, groups: Word, 79; Subject, 21; Page, 10
## Fixed Effects:
## (Intercept) scTrial
## -0.2701 -0.0385
## NativeLanguageOther Classplant
## 0.7052 0.0416
## NativeLanguageOther:Classplant
## -0.1696
( model_r2 <- lmer(scRT ~ scTrial + NativeLanguage*Class +
(1 | Subject) + (1 | Page ) + (1 | Word),
data = lexdec_corr) )
## Linear mixed model fit by REML ['lmerMod']
## Formula: scRT ~ scTrial + NativeLanguage * Class + (1 | Subject) + (1 |
## Page) + (1 | Word)
## Data: lexdec_corr
## REML criterion at convergence: 3599.746
## Random effects:
## Groups Name Std.Dev.
## Word (Intercept) 0.3265
## Subject (Intercept) 0.5319
## Page (Intercept) 0.2869
## Residual 0.6942
## Number of obs: 1594, groups: Word, 79; Subject, 21; Page, 10
## Fixed Effects:
## (Intercept) scTrial
## -0.27083 -0.03727
## NativeLanguageOther Classplant
## 0.70558 0.04608
## NativeLanguageOther:Classplant
## -0.18058
( model_r3 <- lmer(scRT ~ scTrial + NativeLanguage*Class +
(1 | Subject) + (1 | Page ),
data = lexdec_corr) )
## Linear mixed model fit by REML ['lmerMod']
## Formula: scRT ~ scTrial + NativeLanguage * Class + (1 | Subject) + (1 |
## Page)
## Data: lexdec_corr
## REML criterion at convergence: 3749.47
## Random effects:
## Groups Name Std.Dev.
## Subject (Intercept) 0.5286
## Page (Intercept) 0.3100
## Residual 0.7557
## Number of obs: 1594, groups: Subject, 21; Page, 10
## Fixed Effects:
## (Intercept) scTrial
## -0.28877 -0.03508
## NativeLanguageOther Classplant
## 0.69806 0.07262
## NativeLanguageOther:Classplant
## -0.18751
# modellek összevetése
anova(model_r3, model_r2, model_r1, model_full, refit = FALSE)
## Data: lexdec_corr
## Models:
## model_r3: scRT ~ scTrial + NativeLanguage * Class + (1 | Subject) + (1 |
## model_r3: Page)
## model_r2: scRT ~ scTrial + NativeLanguage * Class + (1 | Subject) + (1 |
## model_r2: Page) + (1 | Word)
## model_r1: scRT ~ scTrial + NativeLanguage * Class + (1 | Subject) + (0 +
## model_r1: scTrial | Subject) + (1 | Page) + (1 | Word)
## model_full: scRT ~ scTrial + NativeLanguage * Class + (1 + scTrial | Subject) +
## model_full: (1 | Page) + (1 | Word)
## Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## model_r3 8 3765.5 3808.5 -1874.7 3749.5
## model_r2 9 3617.7 3666.1 -1799.9 3599.7 149.724 1 < 2e-16 ***
## model_r1 10 3596.3 3650.1 -1788.2 3576.3 23.423 1 1.3e-06 ***
## model_full 11 3596.0 3655.1 -1787.0 3574.0 2.365 1 0.1241
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# AIC
AIC(model_r3, model_r2, model_r1, model_full)
## df AIC
## model_r3 8 3765.470
## model_r2 9 3617.746
## model_r1 10 3596.323
## model_full 11 3595.958
# BIC
BIC(model_r3, model_r2, model_r1, model_full)
## df BIC
## model_r3 8 3808.462
## model_r2 9 3666.112
## model_r1 10 3650.063
## model_full 11 3655.072
Random hatások ellenőrzése
- BLUP (best linear unbiased predictor) -> Douglas Bates inkább a "conditional mode of random effects" megfogalmazást preferálja
- a legjobb, ha a feltételes variancia-kovariancia mátrixot is kérjük, de ez többtagú random hatásoknál egyelőre nem működik
ranefs <- ranef(model_r1, condVar = TRUE)
## Warning in ranef.merMod(model_r1, condVar = TRUE): conditional variances
## not currently available via ranef when there are multiple terms per factor
library(lattice) # az ábrázoláshoz betöltjük a lattice csomagot
dotplot(ranefs)
## $Word
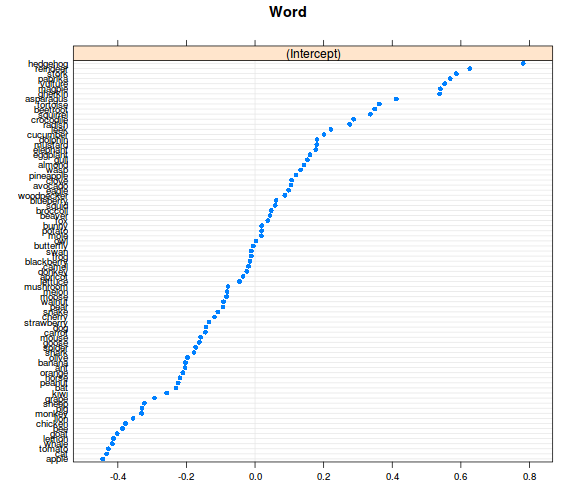
##
## $Subject
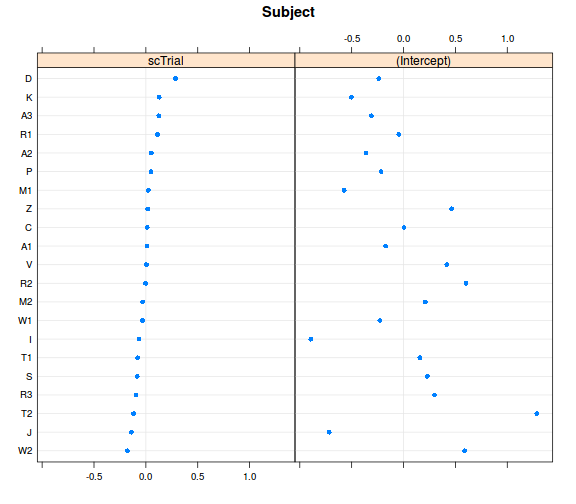
##
## $Page
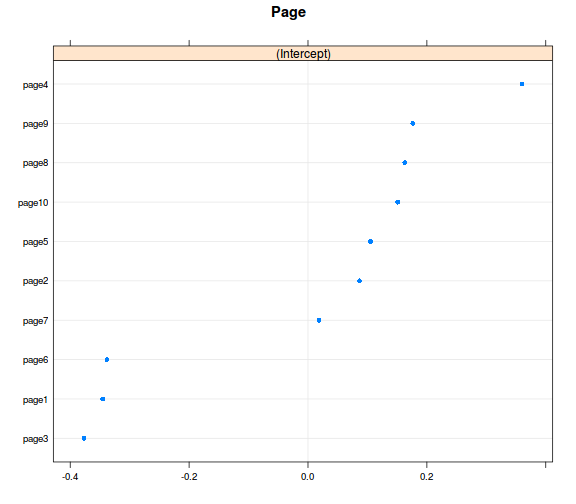
# ennél a modellnél stimmel a dolog
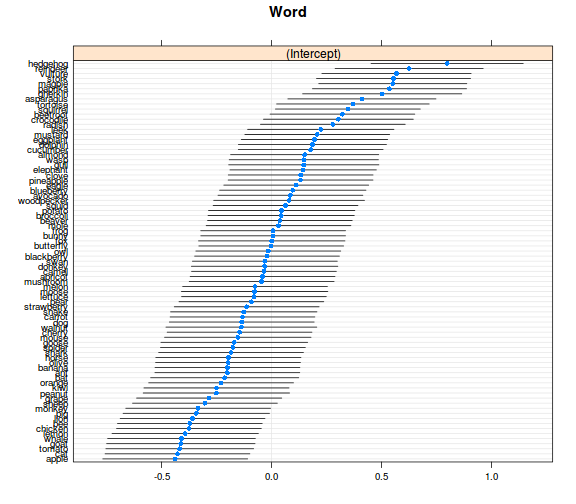
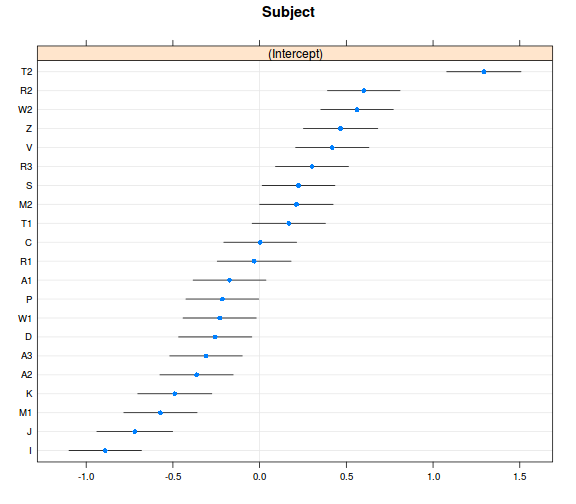
ranefs_vcov <- ranef(model_r2, condVar = TRUE)
dotplot(ranefs_vcov)
## $Word
##
## $Subject
##
## $Page
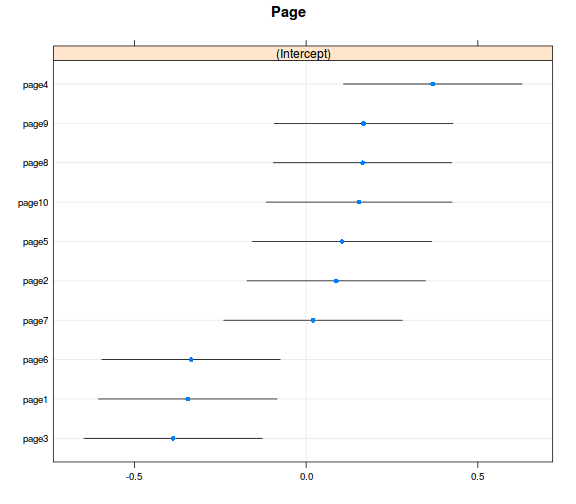
- összességében azt látjuk, hogy a random hatások valóban számottevő mértékűek
- ellenőrizzük a reziduálisokat (normál eloszlásúak-e, van-e szélsőséges érték):
resids <- scale(residuals(model_r1))
par(mfrow = c(1, 2))
hist(resids) # sima hisztogram
qqnorm(resids) # Q-Q ábra a normalitás ellenőrzésére
qqline(resids)
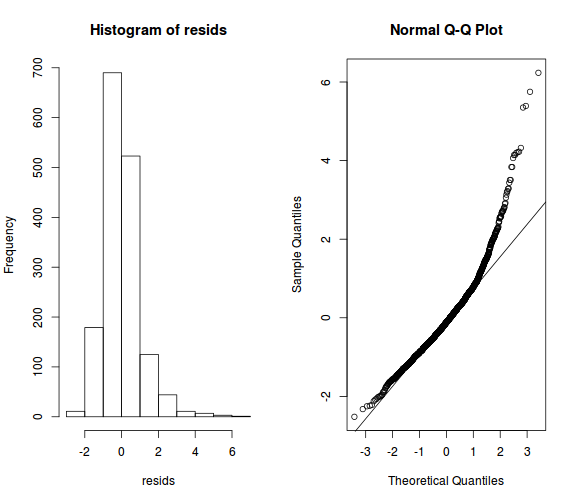
- a reziduálisok alapján megfontolandó lenne, hogy a válaszidők logaritmusa helyett azok inverz transzformáltjával számoljunk, vagy esetleg zárjuk ki azokat az eseteket, amelyeknél a standardizált reziduális túllép egy bizonyos értéket (pl. 2,5-öt)
- válasszuk ki a végső modellt
model_ranef_final <- model_r1
Fix hatások tesztelése
- a legkényelmesebb módszer: best subset; FIGYELEM, ésszel használjuk!!!
- mivel most a fix hatásokat teszteljük, sima ML becslést (nem pedig REML-t) kell alkalmazni
library(MuMIn)
options(na.action = "na.fail") # ez kell, különben a dredge fv. panaszkodik
# Alapesetben az ML megoldható az update() függvénnyel
model_ranef_final_ml <- update(model_ranef_final, REML = FALSE)
# Modellek illesztése
( fixmodels <- dredge(model_ranef_final_ml) )
## Fixed term is "(Intercept)"
## Global model call: lmer(formula = scRT ~ scTrial + NativeLanguage * Class + (1 |
## Subject) + (0 + scTrial | Subject) + (1 | Page) + (1 | Word),
## data = lexdec_corr, REML = FALSE)
## ---
## Model selection table
## (Int) Cls NtL scT Cls:NtL df logLik AICc delta weight
## 12 -0.26930 + + + 9 -1781.578 3581.3 0.00 0.364
## 16 -0.26960 + + -0.03846 + 10 -1780.872 3581.9 0.61 0.268
## 3 -0.25140 + 7 -1784.564 3583.2 1.93 0.139
## 7 -0.25120 + -0.03836 8 -1783.873 3583.8 2.57 0.101
## 4 -0.23720 + + 8 -1784.498 3585.1 3.82 0.054
## 8 -0.23740 + + -0.03826 9 -1783.811 3585.7 4.47 0.039
## 1 0.01855 6 -1787.815 3587.7 6.41 0.015
## 5 0.01856 -0.03839 7 -1787.122 3588.3 7.04 0.011
## 2 0.03267 + 7 -1787.750 3589.6 8.30 0.006
## 6 0.03227 + -0.03828 8 -1787.060 3590.2 8.94 0.004
## Models ranked by AICc(x)
## Random terms (all models):
## '1 | Subject', '0 + scTrial | Subject', '1 | Page', '1 | Word'
- az eredmények azt mutatják, hogy a Trial változónk hatása nem szignifikáns, és erősen határeset a Class főhatása és a NativaLanguage X Class interakció is
- tegyuk fel, hogy az scTrial-t kontrollváltozóként mindenképpen szerepeltetni akarjuk, és kérjük a BIC kritériumot is
( fixmodels2 <- dredge(model_ranef_final_ml,
rank = "AIC", extra = "BIC", fix = "scTrial") )
## Fixed terms are "scTrial" and "(Intercept)"
## Global model call: lmer(formula = scRT ~ scTrial + NativeLanguage * Class + (1 |
## Subject) + (0 + scTrial | Subject) + (1 | Page) + (1 | Word),
## data = lexdec_corr, REML = FALSE)
## ---
## Model selection table
## (Int) Cls NtL scT Cls:NtL BIC df logLik AIC delta weight
## 8 -0.26960 + + -0.03846 + 3635 10 -1780.872 3581.7 0.00 0.639
## 3 -0.25120 + -0.03836 3627 8 -1783.873 3583.7 2.00 0.235
## 4 -0.23740 + + -0.03826 3634 9 -1783.811 3585.6 3.88 0.092
## 1 0.01856 -0.03839 3626 7 -1787.122 3588.2 6.50 0.025
## 2 0.03227 + -0.03828 3633 8 -1787.060 3590.1 8.38 0.010
## Models ranked by AIC(x)
## Random terms (all models):
## '1 | Subject', '0 + scTrial | Subject', '1 | Page', '1 | Word'
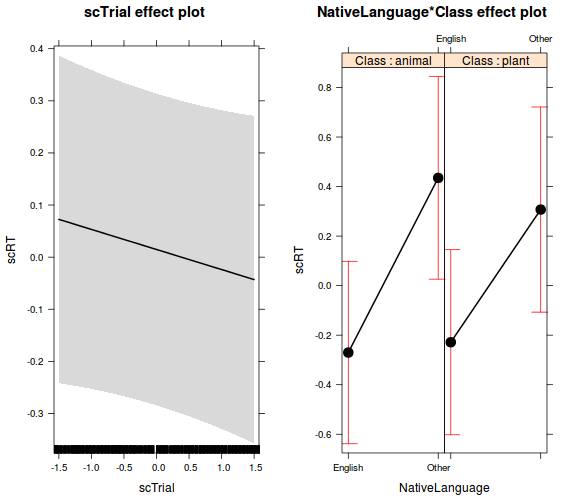
Fix hatások ábrázolása
- az effects package mindenféle modellre (köztük a merMod modellekre is) tud ábrát készíteni
library(effects)
effs <- allEffects(model_ranef_final)
plot(effs)
## Loading required package: grid
## Loading required package: colorspace
##
## Attaching package: 'effects'
##
## The following object is masked from 'package:car':
##
## Prestige