Adatexploráció, ábrázolás
A kísérleti dizájn vizsgálata, leíró statisztikák
- elvileg keresztezett random hatásaink vannak: minden személynek minden szót bemutattak, pontosan egyszer
freq <- with(lexdec, table(Subject, Word))
# a freq mátrix túl nagy, a példához elég egy kis részlete
freq[1:5, 1:5]
## Word
## Subject almond ant apple apricot asparagus
## A1 1 1 1 1 1
## A2 1 1 1 1 1
## A3 1 1 1 1 1
## C 1 1 1 1 1
## D 1 1 1 1 1
# tökéletesen keresztezett, ismétlés nélküli dizájn
table(freq)
## freq
## 1
## 1659
- létrehoztunk egy beágyazott hatást is: a szavak a szótár egy-egy oldaláról származnak
with(lexdec, table(Word, Page))
## Page
## Word page1 page2 page3 page4 page5 page6 page7 page8 page9 page10
## almond 21 0 0 0 0 0 0 0 0 0
## ant 21 0 0 0 0 0 0 0 0 0
## apple 21 0 0 0 0 0 0 0 0 0
## apricot 21 0 0 0 0 0 0 0 0 0
## asparagus 21 0 0 0 0 0 0 0 0 0
## avocado 21 0 0 0 0 0 0 0 0 0
## banana 21 0 0 0 0 0 0 0 0 0
## bat 21 0 0 0 0 0 0 0 0 0
## beaver 0 21 0 0 0 0 0 0 0 0
## bee 0 21 0 0 0 0 0 0 0 0
## beetroot 0 21 0 0 0 0 0 0 0 0
## blackberry 0 21 0 0 0 0 0 0 0 0
## blueberry 0 21 0 0 0 0 0 0 0 0
## broccoli 0 21 0 0 0 0 0 0 0 0
## bunny 0 21 0 0 0 0 0 0 0 0
## butterfly 0 21 0 0 0 0 0 0 0 0
## camel 0 0 21 0 0 0 0 0 0 0
## carrot 0 0 21 0 0 0 0 0 0 0
## cat 0 0 21 0 0 0 0 0 0 0
## cherry 0 0 21 0 0 0 0 0 0 0
## chicken 0 0 21 0 0 0 0 0 0 0
## clove 0 0 21 0 0 0 0 0 0 0
## crocodile 0 0 21 0 0 0 0 0 0 0
## cucumber 0 0 21 0 0 0 0 0 0 0
## dog 0 0 0 21 0 0 0 0 0 0
## dolphin 0 0 0 21 0 0 0 0 0 0
## donkey 0 0 0 21 0 0 0 0 0 0
## eagle 0 0 0 21 0 0 0 0 0 0
## eggplant 0 0 0 21 0 0 0 0 0 0
## elephant 0 0 0 21 0 0 0 0 0 0
## fox 0 0 0 21 0 0 0 0 0 0
## frog 0 0 0 21 0 0 0 0 0 0
## gherkin 0 0 0 0 21 0 0 0 0 0
## goat 0 0 0 0 21 0 0 0 0 0
## goose 0 0 0 0 21 0 0 0 0 0
## grape 0 0 0 0 21 0 0 0 0 0
## gull 0 0 0 0 21 0 0 0 0 0
## hedgehog 0 0 0 0 21 0 0 0 0 0
## horse 0 0 0 0 21 0 0 0 0 0
## kiwi 0 0 0 0 21 0 0 0 0 0
## leek 0 0 0 0 0 21 0 0 0 0
## lemon 0 0 0 0 0 21 0 0 0 0
## lettuce 0 0 0 0 0 21 0 0 0 0
## lion 0 0 0 0 0 21 0 0 0 0
## magpie 0 0 0 0 0 21 0 0 0 0
## melon 0 0 0 0 0 21 0 0 0 0
## mole 0 0 0 0 0 21 0 0 0 0
## monkey 0 0 0 0 0 21 0 0 0 0
## moose 0 0 0 0 0 0 21 0 0 0
## mouse 0 0 0 0 0 0 21 0 0 0
## mushroom 0 0 0 0 0 0 21 0 0 0
## mustard 0 0 0 0 0 0 21 0 0 0
## olive 0 0 0 0 0 0 21 0 0 0
## orange 0 0 0 0 0 0 21 0 0 0
## owl 0 0 0 0 0 0 21 0 0 0
## paprika 0 0 0 0 0 0 21 0 0 0
## peanut 0 0 0 0 0 0 0 21 0 0
## pear 0 0 0 0 0 0 0 21 0 0
## pig 0 0 0 0 0 0 0 21 0 0
## pineapple 0 0 0 0 0 0 0 21 0 0
## potato 0 0 0 0 0 0 0 21 0 0
## radish 0 0 0 0 0 0 0 21 0 0
## reindeer 0 0 0 0 0 0 0 21 0 0
## shark 0 0 0 0 0 0 0 21 0 0
## sheep 0 0 0 0 0 0 0 0 21 0
## snake 0 0 0 0 0 0 0 0 21 0
## spider 0 0 0 0 0 0 0 0 21 0
## squid 0 0 0 0 0 0 0 0 21 0
## squirrel 0 0 0 0 0 0 0 0 21 0
## stork 0 0 0 0 0 0 0 0 21 0
## strawberry 0 0 0 0 0 0 0 0 21 0
## swan 0 0 0 0 0 0 0 0 21 0
## tomato 0 0 0 0 0 0 0 0 0 21
## tortoise 0 0 0 0 0 0 0 0 0 21
## vulture 0 0 0 0 0 0 0 0 0 21
## walnut 0 0 0 0 0 0 0 0 0 21
## wasp 0 0 0 0 0 0 0 0 0 21
## whale 0 0 0 0 0 0 0 0 0 21
## woodpecker 0 0 0 0 0 0 0 0 0 21
Fontos, hogy sose kódoljunk úgy változókat, hogy ne legyen egyértelmű, hogy keresztezett vagy beágyazott hatásokról van-e szó. Magyarán ha hierarchikus változóink vannak (pl. személy << iskola, vagy jelen példában szó << szótári oldal), akkor az alsóbb szinten is alkalmazzunk egyedi azonosítókat. Jelen példánál maradva, ahol minden szótári oldalról 8-8 szó szerepel, hiba lenne a szavakat "word1", "word2", "word3", ..., "word8"-ként kódolni, hiszen az egyik oldal "word1" szavának semmi köze nincsen a másik oldal "word1" szavához.
# tegyük fel, hogy a Word változót word1, word2, ... word8-ként kódoltuk
# a Page minden szintjén
lexdec$WordWrong <- paste0(
"word",
as.integer(lexdec$Word) - 8*(as.integer(lexdec$Page)-1))
# innentől a keresztgyakorisági tábla nem mutatja meg, hogy
# a 'word' faktor a 'page' faktorunkba van ágyazva
with(lexdec, table(WordWrong, Page))
## Page
## WordWrong page1 page2 page3 page4 page5 page6 page7 page8 page9 page10
## word1 21 21 21 21 21 21 21 21 21 21
## word2 21 21 21 21 21 21 21 21 21 21
## word3 21 21 21 21 21 21 21 21 21 21
## word4 21 21 21 21 21 21 21 21 21 21
## word5 21 21 21 21 21 21 21 21 21 21
## word6 21 21 21 21 21 21 21 21 21 21
## word7 21 21 21 21 21 21 21 21 21 21
## word8 21 21 21 21 21 21 21 21 21 0
- csak a helyes válaszokat akarjuk elemezni: szűrjük le az adatokat és válasszuk ki a releváns változókat
lexdec_corr <- subset(lexdec, Correct == "correct",
select = c(Subject, RT, Trial, NativeLanguage,
Word, Class, Page))
- kérjünk leíró statisztikákat a kérdéses változókra (a psych csomagot fogom használni, de egyebet is lehetne)
# általános leíró statisztikák
summary(lexdec_corr)
## Subject RT Trial NativeLanguage
## A3 : 79 Min. :5.816 Min. : 23.0 English:920
## I : 79 1st Qu.:6.227 1st Qu.: 64.0 Other :674
## R2 : 79 Median :6.364 Median :106.0
## W2 : 79 Mean :6.397 Mean :104.9
## A1 : 78 3rd Qu.:6.526 3rd Qu.:146.0
## C : 78 Max. :7.444 Max. :185.0
## (Other):1122
## Word Class Page
## ant : 21 animal:884 page2 :166
## apple : 21 plant :710 page3 :165
## apricot: 21 page6 :164
## avocado: 21 page8 :163
## banana : 21 page1 :162
## beaver : 21 page4 :162
## (Other):1468 (Other):612
# példa: válaszidők statisztikái szavanként, ferdeségi mutatóval
with(lexdec_corr, psych::describeBy(RT, Subject, skew = TRUE))
## group: A1
## vars n mean sd median trimmed mad min max
## 1 1 78 6.29445 0.2371747 6.251629 6.275394 0.196216 5.816334 7.08423
## range skew kurtosis se
## 1 1.267896 0.8520839 0.7785435 0.02685475
## --------------------------------------------------------
## group: A2
## vars n mean sd median trimmed mad min max
## 1 1 76 6.241644 0.1812018 6.210338 6.226239 0.1322974 5.859236 6.749907
## range skew kurtosis se
## 1 0.890671 0.8430157 0.7210964 0.02078528
## --------------------------------------------------------
## group: A3
## vars n mean sd median trimmed mad min max
## 1 1 79 6.411508 0.174746 6.405334 6.397683 0.1537506 6.089654 7.20633
## range skew kurtosis se
## 1 1.116676 1.585181 5.124337 0.01966046
## --------------------------------------------------------
## group: C
## vars n mean sd median trimmed mad min max
## 1 1 78 6.336761 0.153622 6.328853 6.333675 0.1715731 6.079752 6.839127
## range skew kurtosis se
## 1 0.7593749 0.4114168 0.02946384 0.01739427
## --------------------------------------------------------
## group: D
## vars n mean sd median trimmed mad min max
## 1 1 76 6.42303 0.2006718 6.386154 6.406292 0.1645523 6.021854 6.989496
## range skew kurtosis se
## 1 0.9676422 0.7265388 0.407637 0.02301863
## --------------------------------------------------------
## group: I
## vars n mean sd median trimmed mad min max
## 1 1 79 6.266895 0.2313842 6.262087 6.250492 0.2156946 5.821799 7.193265
## range skew kurtosis se
## 1 1.371466 0.9771252 2.260001 0.02603276
## --------------------------------------------------------
## group: J
## vars n mean sd median trimmed mad min max
## 1 1 67 6.293374 0.1738307 6.285565 6.282037 0.1597834 5.958208 6.866369
## range skew kurtosis se
## 1 0.9081612 0.8146107 1.120534 0.0212368
## --------------------------------------------------------
## group: K
## vars n mean sd median trimmed mad min max
## 1 1 73 6.213245 0.1679288 6.201764 6.200523 0.1496421 5.871196 6.645689
## range skew kurtosis se
## 1 0.7744929 0.5962026 0.01302904 0.01965457
## --------------------------------------------------------
## group: M1
## vars n mean sd median trimmed mad min max
## 1 1 76 6.189777 0.1489886 6.184 6.179755 0.1240525 5.958208 6.991805
## range skew kurtosis se
## 1 1.033596 1.971881 8.960611 0.01709017
## --------------------------------------------------------
## group: M2
## vars n mean sd median trimmed mad min max
## 1 1 75 6.534821 0.2842884 6.478462 6.502254 0.2075407 6.126521 7.436621
## range skew kurtosis se
## 1 1.3101 1.169999 1.369175 0.0328268
## --------------------------------------------------------
## group: P
## vars n mean sd median trimmed mad min max
## 1 1 78 6.435114 0.2028893 6.437196 6.417274 0.18803 6.090088 7.003854
## range skew kurtosis se
## 1 0.9137665 0.7444783 0.2491568 0.02297269
## --------------------------------------------------------
## group: R1
## vars n mean sd median trimmed mad min max
## 1 1 74 6.321197 0.2096948 6.277186 6.296668 0.1251596 5.918769 7.443722
## range skew kurtosis se
## 1 1.524954 2.513418 10.28148 0.02437652
## --------------------------------------------------------
## group: R2
## vars n mean sd median trimmed mad min max
## 1 1 79 6.486008 0.1487251 6.479719 6.484601 0.1409063 6.079392 6.945922
## range skew kurtosis se
## 1 0.8665307 0.1315091 0.4415866 0.01673288
## --------------------------------------------------------
## group: R3
## vars n mean sd median trimmed mad min max
## 1 1 77 6.407649 0.1910904 6.398014 6.402558 0.2024326 6.068556 6.889455
## range skew kurtosis se
## 1 0.8208992 0.285513 -0.7359847 0.02177678
## --------------------------------------------------------
## group: S
## vars n mean sd median trimmed mad min max
## 1 1 78 6.388921 0.2227348 6.331799 6.37157 0.1885148 5.942303 7.058474
## range skew kurtosis se
## 1 1.116171 0.8178309 0.4936526 0.02521975
## --------------------------------------------------------
## group: T1
## vars n mean sd median trimmed mad min max
## 1 1 76 6.378826 0.1838232 6.369693 6.36946 0.1618263 6.018996 7.199115
## range skew kurtosis se
## 1 1.180119 1.106364 3.542694 0.02108597
## --------------------------------------------------------
## group: T2
## vars n mean sd median trimmed mad min max
## 1 1 72 6.803464 0.2281968 6.81935 6.800709 0.2415011 6.289565 7.382824
## range skew kurtosis se
## 1 1.093259 0.08222496 -0.3742787 0.02689325
## --------------------------------------------------------
## group: V
## vars n mean sd median trimmed mad min max
## 1 1 76 6.586475 0.1856749 6.561587 6.575127 0.1947326 6.308967 7.117976
## range skew kurtosis se
## 1 0.8090095 0.5560653 -0.3809575 0.02129837
## --------------------------------------------------------
## group: W1
## vars n mean sd median trimmed mad min
## 1 1 76 6.272456 0.1251487 6.252294 6.260596 0.08296481 6.062139
## max range skew kurtosis se
## 1 6.669786 0.6076469 0.9484034 0.7339698 0.01435554
## --------------------------------------------------------
## group: W2
## vars n mean sd median trimmed mad min max
## 1 1 79 6.47424 0.2011546 6.45066 6.465565 0.2086125 6.100586 7.064089
## range skew kurtosis se
## 1 0.9635033 0.498012 0.01056057 0.02263167
## --------------------------------------------------------
## group: Z
## vars n mean sd median trimmed mad min max
## 1 1 72 6.598258 0.2370327 6.583337 6.585071 0.2574446 6.170266 7.16909
## range skew kurtosis se
## 1 0.998824 0.4364043 -0.5002696 0.02793457
Ábrázolás
A következőkben ggplot ábrákkal megvizsgáljuk, hogy milyen a hiányzó adatok mintázata, illetve hogyan alakul a válaszidők eloszlása különböző csoportosító szempontok alapján.
- hiányzó adatok (amiatt, hogy csak a helyes válaszokat elemezzük):
library(ggplot2)
ggplot(lexdec_corr, aes(x = Subject, y = Word)) +
geom_tile()
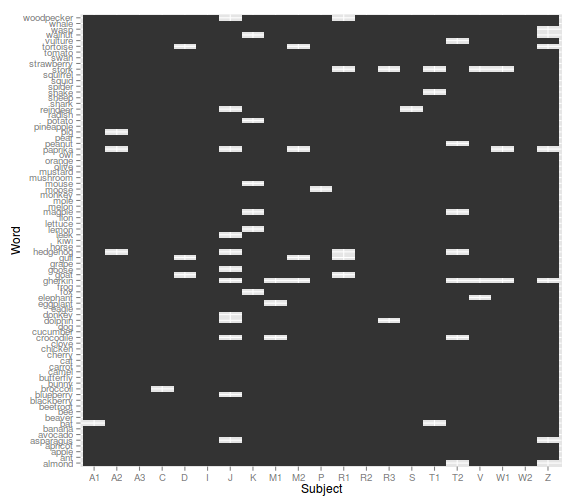
- válaszidők személyenként:
# Subject
ggplot(lexdec_corr, aes(x = Subject, y = RT, col = NativeLanguage)) +
geom_boxplot() +
theme_bw()
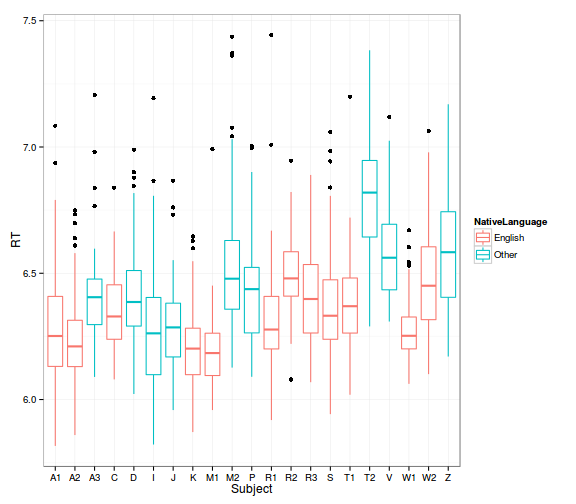
- válaszidők szavanként és oldalanként
# Page & Word
ggplot(lexdec_corr, aes(x = Word, y = RT, col = Page)) +
geom_boxplot() +
theme_bw() +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
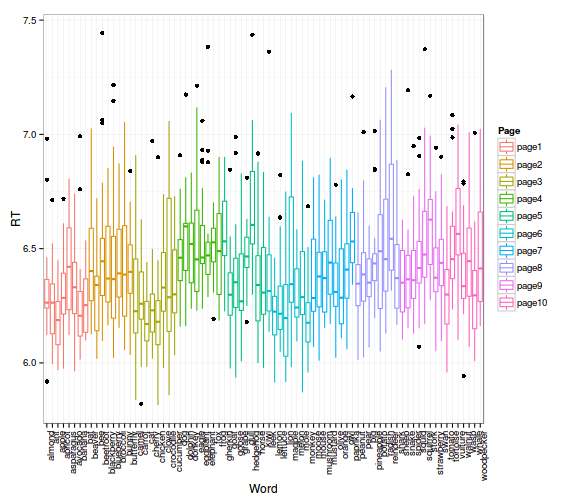
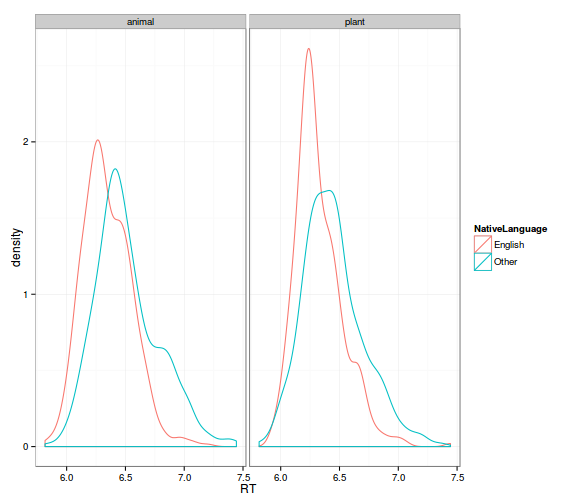
- válaszidők eloszlása az anyanyelv és az ingerosztály (állat/növény) függvényében
# Class & NativeLanguage (boxplot)
ggplot(lexdec_corr, aes(x = NativeLanguage, y = RT, col = Class)) +
geom_boxplot() +
theme_bw()
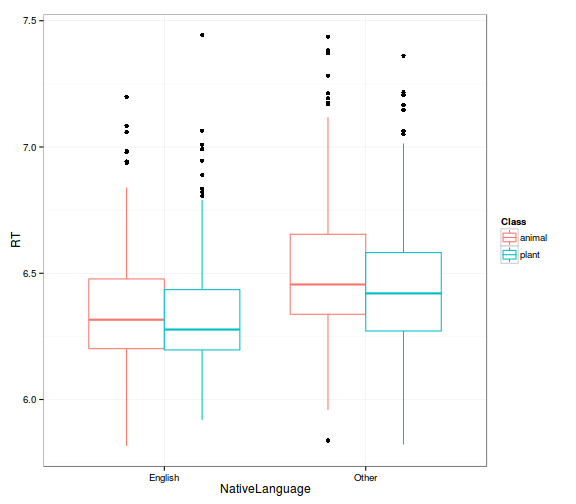
# Class & NativeLanguage (density)
ggplot(lexdec_corr, aes(x = RT, col = NativeLanguage)) +
geom_density() +
facet_wrap(~ Class) +
theme_bw()
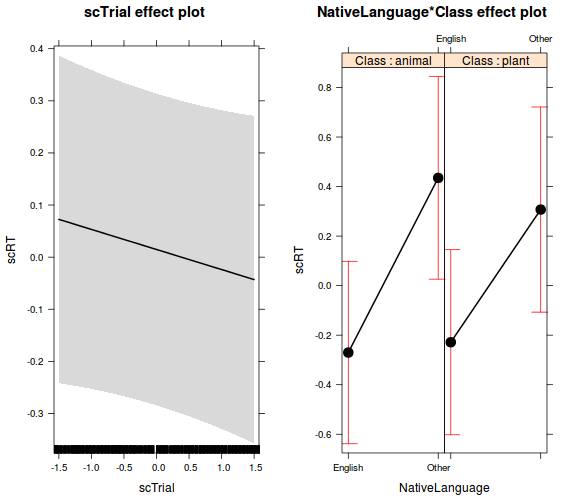
- a Trial változó hatása
# Trial
ggplot(lexdec_corr, aes(x = Trial, y = RT)) +
geom_point() +
stat_smooth(method = "lm") +
facet_wrap(~Subject) +
theme_bw()
Adatok előkészítése
- ha lennének egyértelmű outlierek, azokat érdemes az elemzés előtt kiszűrni
- standardizálhatjuk a folytonos változókat
lexdec_corr[, c("scRT", "scTrial")] <- scale(lexdec_corr[, c("RT", "Trial")])
- az elemzési céljainktól függ, de érdemes lehet átállítani a kontrasztokat (az R alapból treatment-kontrasztot használ)
op <- options(contrasts = c("contr.sum", "contr.poly"))